Summary
I am a Postdoctoral Research Assistant at UCL . Prior to that, I was a DPhil student in the Numerical Analysis Group at the University of Oxford, and I am affiliated with Worcester College. I am conducting my research under the supervision of Prof. Raphael Hauser. My research interests are related to optimisation under uncertainty and game theory applied to energy.Before my DPhil, I obtained a MSc in Mathematical Engineering from the Université catholique de Louvain (Belgium) and a MSc in Engineering from the Ecole Centrale de Paris (France). During my MSc thesis, which I undertook under the supervision of Prof. Anthony Papavasiliou, I designed a primal heuristic applied to the optimal transmission expansion planning problem.
Publications
With V. M. Charitopoulos.
Computer Aided Chemical Engineering, 2023 (to appear). Preprint link PDF
@article{Vaes2022e,
archivePrefix = {arXiv},
arxivId = {2212.01478},
author = {Vaes, Julien and Charitopoulos, Vassilis M.},
eprint = {2212.01478},
pages = {1--8},
title = {{A data-driven uncertainty modelling and reduction approach for energy optimisation problems}},
url = {http://arxiv.org/abs/2212.01478},
year = {2022}
}With R. Hauser.
In preparation.
With R. Hauser.
In preparation.
With R. Hauser.
In preparation.
With R. Hauser.
Journal of Computational Finance, 2022. Preprint link Publisher link
@article{Vaes2022,
author = {Vaes, Julien and Hauser, Raphael},
doi = {10.21314/JCF.2022.018},
journal = {Journal of Computational Finance},
number = {1},
title = {{Optimal trade execution with uncertain volume target}},
volume = {26},
year = {2022},
}The trading cost \( \mathcal{C}({\bf{y}}) \) of a strategy \({\bf{y}}\) is then defined as the difference between (i) the cost incurred at the end of the execution period by following the trading strategy \( {\bf{y}} \) with (ii) the cost ideally obtained in an infinitely liquid market where the entire position \( D_{t_b} \) is traded at the start of the execution period. In Almgren and Chriss (2001), it is assumed that a risk-averse trader desires to minimise the trade-off of the expectation and the variance of the trading cost of their strategy, i.e. \[ \begin{align} \text{minimise}_{{\bf{y}}} &&& \mathbb{E} \left[ \mathcal{C}({\bf{y}}) \right] + \lambda \, \mathbb{V} \left[ \mathcal{C}({\bf{y}}) \right],\\ \text{such that} &&& \sum_{i = 1}^m y_i = 1, \end{align} \] where \(\lambda\) is the risk-aversion parameter; the larger \(\lambda\), the more risk-averse the trader. The figure here under illustrate the optimal strategy in the mean-variance framework when the risk-aversion parameter increases; the larger \(\lambda\), the more front loading in order to avoid risk associated with the price dynamics.
As the variance of the trading cost of a trader is not of foremost importance if they are guaranteed to not pay excessive prices in adverse times, it is often assumed that a trader should evaluate their risk with the Conditional Value-at-Risk (CVaR) risk measure. This translates the idea that a trader is more interested in minimising their expected trading cost conditional to a quantile of worst case scenarios rather than minimising the variance of their trading cost over all scenarios. A trader would then solve the following optimisation problem in order to define their optimal trading strategy, \[ \begin{align} \text{minimise}_{{\bf{y}}} &&& (1-\lambda) \, \mathbb{E} \left[ \mathcal{C}({\bf{y}}) \right] + \lambda \, \text{CVaR}_{\alpha} \left[ \mathcal{C}({\bf{y}}) \right],\\ \text{such that} &&& \sum_{i = 1}^m y_i = 1, \end{align} \] where \(\text{CVaR}_{\alpha} \left[ \mathcal{C}({\bf{y}}) \right]\) can be interpreted as the expectation of the costs conditional on them belonging to the \(\alpha\)% largest trading costs. Here, a value of \(\lambda = 0\) corresponds to a risk-neutral trader, where a value of \(\lambda = 1\) corresponds to an exclusively risk-focused trader.
Given the market parameters assumed in our paper Vaes and Hauser (2018), the following graph and table present respectively the optimal strategies and their corresponding performance given different risk-aversion parameter \(\lambda\). We can notice, similarly to the Mean-Variance framework, that the more risk-averse a trader, the quicker the acquisition of the desired positions.

Optimal strategy when considering price uncertainty together with the uncertainty associated with the volume target (Vaes and Hauser, 2018). When the uncertainty related to the volume target is considered in the model detailed in our paper, one obtains the optimal strategies illustrated in the following figure. When comparing the values of the table here under with the previous table, one achieves significant cost reductions.

Impact of the uncertainty associated with the volume target. The following figure illustrates how the optimal strategies obtained when considering exclusively price uncertainty must be adapted to additionally consider the uncertainty related to the volume target. One observes that, in accordance with intuition, waiting for a better volume forecast is beneficial in terms of risk reduction.
PhD thesis supervised by R. Hauser.
Soon available on Oxford University Research Archive (ORA), 2022.
@phdthesis{Vaes2022d,
author = {Vaes, Julien},
school = {University of Oxford},
title = {{Risk-averse Nash equilibria for power trading with market frictions}},
year = {2022}
}MSc thesis supervised by A. Papavasiliou.
Available on UCLouvain's website, 2017. Publisher link
@mastersthesis{Vaes2017,
author = {Vaes, Julien and Papavasiliou, Anthony},
title = {{Optimal transmission expansion planning}},
year = {2017},
school = {Universit\'e catholique de Louvain},
url = {https://dial.uclouvain.be/memoire/ucl/en/object/thesis%3A12931},
}Talks and posters
Teaching
Other projects
Based on an optimization approach, we have investigated whether we could find a running trajectory for a home run in baseball that is faster than the 16.7 seconds theoretical limit stated in the following article. We assume that the runner has finite velocity and acceleration. We show that it is impossible for a runner to accomplish a home run faster than in 15.5 seconds, but we also found out that the limit of 16.7 could be beaten. The following figures illustrate the optimal paths when considering different sets of constraints. (Credit: Prof. F. Glineur)
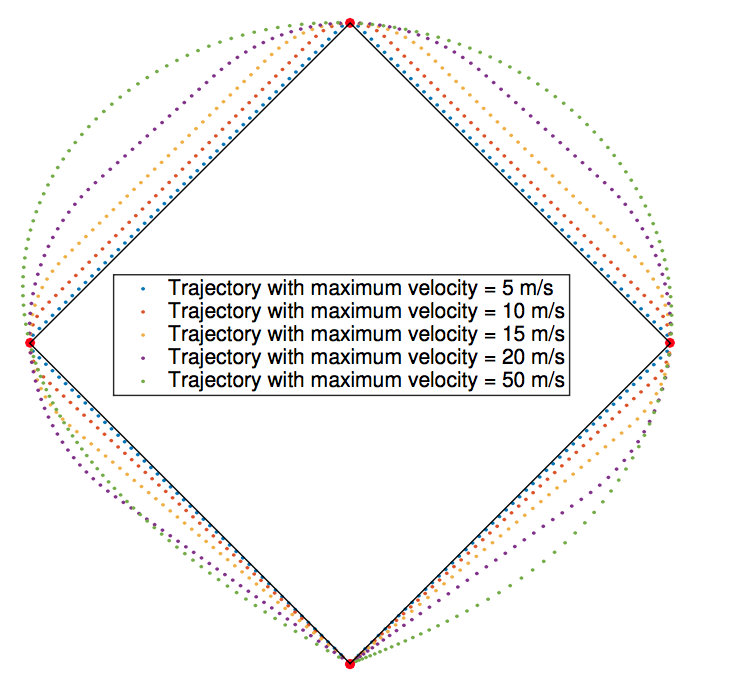
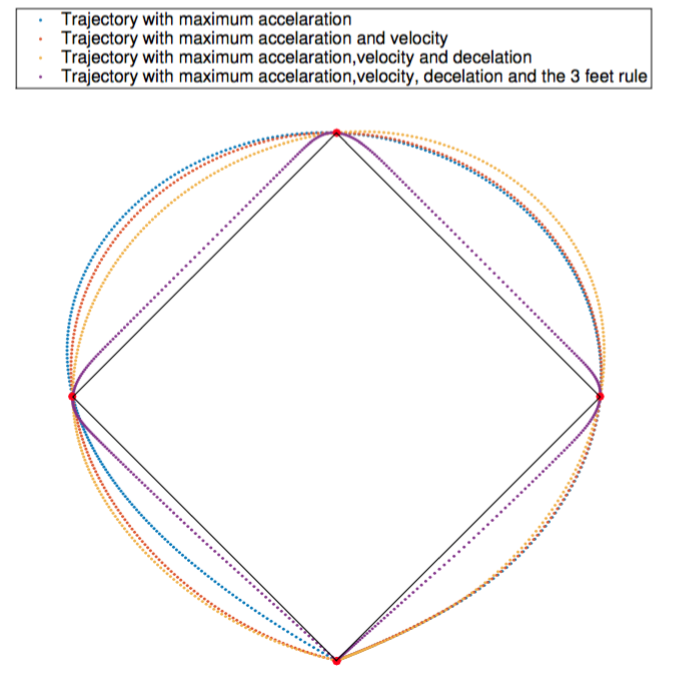
In 2011, Japan has been severly hit by a tsunami, which damaged tremedously the coast of the country. The idea of this project is to better understand how the tsunami propagated based on a numerical simulation. (Credit: Prof. V. Legat)